Intersección

Si dos planos b y a se cortan, lo hacen por una recta a que pasa por dos puntos: la intersección de las trazas Ta de los planos: ta y tb y la intersección de las rectas límites l’a y l’b, ya que las trazas de los planos pasan por el mismo plano, esto es, el plano del cuadro, se cortarán necesariamente en el punto de intersección de éstas. De igual forma, las rectas límites son la imagen de las rectas del infinito de los planos pero están sobre el plano del cuadro y sus puntos corresponden a puntos reales de los mismos, por lo que la intersección L’a de las rectas límites l’a y l’b es un punto de intersección del infinito común a los dos planos.
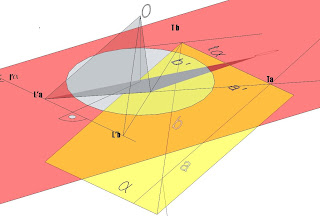
El plano amarillo y rojo (b y a ) se cortan según la recta a. La dirección de la recta a la define la dirección O-L’a y le recta queda definida por los dos puntos Ta-L’a, puntos comunes a los dos planos.












Aquí tenemos la representación en proyección central de los dos planos con su recta de intersección en proyección central: a’ y su representación ortogonal real sobre el plano del cuadro a, que es la intersección efectiva de los dos planos en proyección ortogonal sobre el PC. La proyección central de la recta a es a’, intersección de a y b, a saber, intersección de ta y t b= Ta e intersección de l’a y l’b= L’a.
La recta a’ queda definida por dos puntos: Ta-L’a, esto es, por el punto de intersección de las trazas de los planos y el punto de intersección de las rectas límites de los planos.












Cualquier punto M de la recta a y por tanto común a los dos planos, tendrá su homólogo o correspondiente M’ sobre a’ y estará alineado con O.













Intersección de recta y plano:

Para calcular la intersección de una recta a con un plano b (en amarillo), se pasa un plano a (rojo) por a, la intersección de los dos planos a y b corta a a en un punto M de la recta a, esa es la intersección de la recta a y el plano b.












En la proyección central observamos la recta a por la que se pasa el plano a y su intersección con b, cuya recta de intersección corta a a’ en M’, punto de intersección de la recta y el plano dados b y a.












Si dos rectas a, b se cortan, determinan un plano, por lo que las trazas y límites de las rectas están en las trazas y límites del plano.











Proyección central de rectas pertenecientes a un plano: